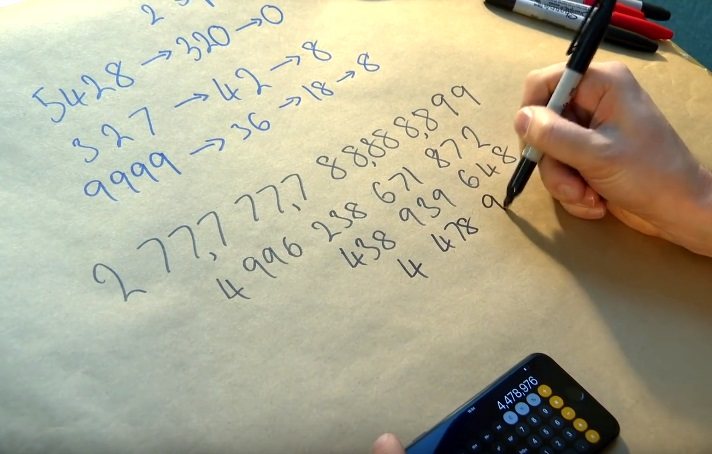La persistencia de un número está definida como la cantidad de veces que aplicamos una operación sobre un entero hasta alcanzar un punto en el que esa operación es incapaz de alterarlo debido a su reducción. Dicha persistencia puede basarse en sumas, o ser multiplicativa, y esta última es la que nos interesa hoy. Una de las prioridades detrás del ejercicio es encontrar a los números más pequeños con mayor cantidad de pasos. La hipótesis vigente sugiere que no existen números con una persistencia superior a 11, y ahí es cuando interviene el extraño 277777788888899. ¿Qué tiene de diferente?
Vamos a hacer una pequeña prueba. Elige un número entero de cuatro dígitos. Yo haré lo mismo aquí, digamos… 7793. Calcular la persistencia multiplicativa de este número es muy sencillo. Todo lo que requiere es multiplicar sus dígitos, tomar el resultado, y repetir el proceso hasta que ya no sea posible. Veamos: 7x7x9x3=1323, 1x3x2x3=18, 1×8=8.
La persistencia multiplicativa de 7793 es de apenas 3 pasos. Ahora, eliminemos la regla de cuatro dígitos, y piensa en un número cualquiera. Tu misión, si es que decides aceptarla, es encontrar uno que supere los 11 pasos de persistencia. Pero ten cuidado: Es mucho más complicado de lo que parece. ¿Qué tal una demostración?
La persistencia de 277777788888899
En un reciente vídeo publicado por el canal Numberphile exploran la peculiar condición de 277777788888899. Una variante interesante para todo el ejercicio es encontrar los números bajos en una persistencia específica, y 277777788888899 es el más pequeño de la persistencia 11.
Al principio dedican un par de minutos al cálculo tradicional, pero aquellos que sepan un poco de programación probablemente estén más interesados en el código que escribe para el cálculo automático. La reducción manual de 2x7x7x7x7x7x7x8x8x8x8x8x8x9x9 sigue este patrón:
- 4996238671872
- 438939648
- 4478976
- 338688
- 27648
- 2688
- 768
- 336
- 54
- 20
- 0
La gran pregunta es si en verdad existe un número con una persistencia mayor a 11. La recomendación que da Numberphile es no buscarlo por debajo de 10^233 (no lo han encontrado), evitar al 5 por completo, y priorizar el uso de 7, 8 y 9. Si sabes escribir código o crees que puedes mejorar el utilizado por Numberphile, quedas invitado.
(Del Archivo de NeoTeo, artículo originalmente el 29 de marzo de 2019)