Imagina que te encuentras en una fiesta, rodeado de una o dos docenas de amigos. ¿Cual es la probabilidad de que un par de ellos cumpla años el mismo día? Aunque parezca increíble, es posible demostrar matemáticamente que si el numero de invitados es de 23 personas, la probabilidad supera el 50%. Y si en tu fiesta hay más de 60 invitados, puedes apostar que dos de ellas cumplen años el mismo día con el 99% de posibilidades de ganar. Bienvenidos a la paradoja del cumpleaños
-
-
Nuevamente estamos ante una de esas contradicciones lógicas, que si bien desde el punto de vista estrictamente matemático no merecen el nombre de “paradoja”, contradicen lo suficiente el sentido común como para que mucha gente las considere como tales. Algo parecido a lo que sucede con la Paradoja de la banda elástica, que analizamos hace algunas semanas. En este caso, además de dejarte pensando un rato sobre algo que seguramente no te habías planteado nunca, conocerás un nuevo truco para convertirte (o no) en el tío más guay de la fiesta.
Hay una buena probabilidad de que al menos dos de ellos cumplan años el mismo día.
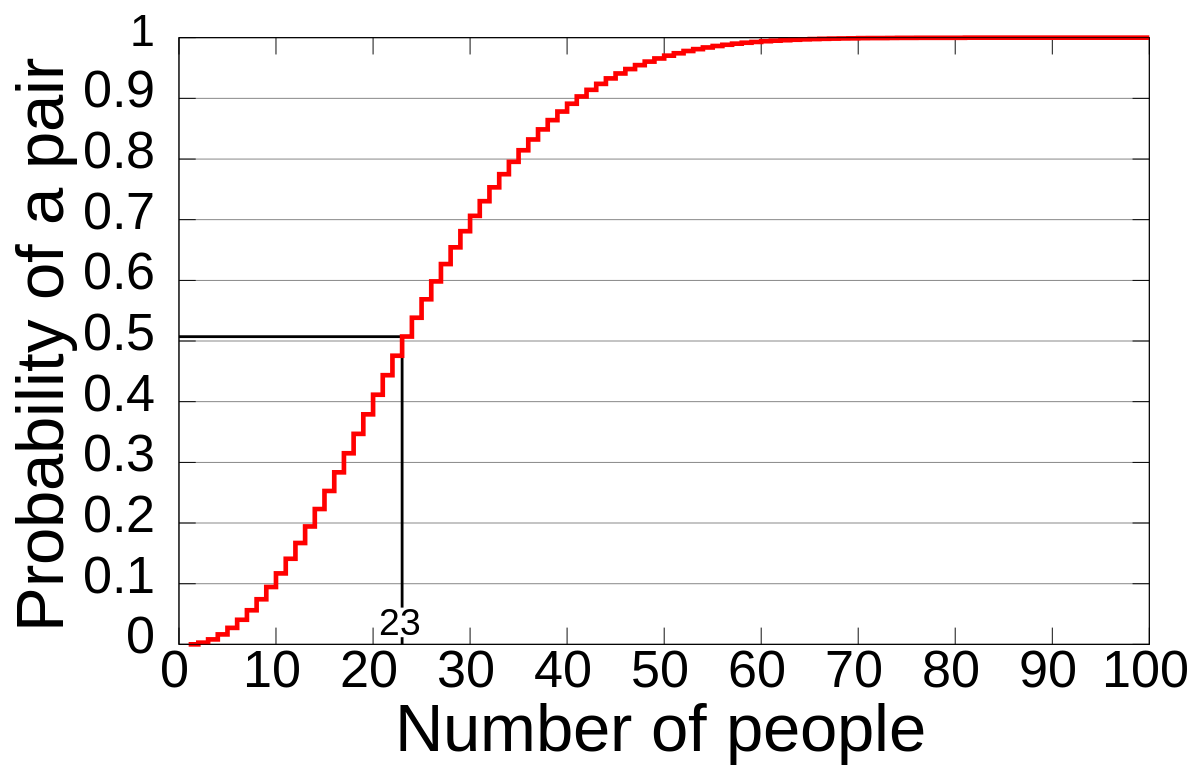
La (mal) llamada Paradoja del cumpleaños establece que si en una reunión se encuentran 23 personas, la probabilidad de que al menos dos de ellas cumplan años el mismo día es del 50,7%. El porcentaje parece, a primera vista, demasiado elevado. Uno tiende a razonar de la siguiente manera: “A ver. El año tiene unos 365 días, y si aquí dentro hay solo 23 personas, pues la probabilidad de que dos de nosotros hayamos nacido el mismo día debe ser de 23/365*100 = 6,3%” ¡Error! ¿En qué nos equivocamos cuando razonamos de esa forma? En que en realidad estamos calculando cual es la probabilidad de que alguno de los presentes cumpla años un día en particular, algo que nada tiene que ver con el problema. Para calcular realmente la probabilidad de dos personas del grupo cumplan años el mismo día hay que considerar parejas y no personas sueltas. Veamos cómo es la forma correcta de hacerlo.
Si. También funciona en una fiesta de pijamas, aunque no lo hemos comprobado.
La clave para entender problema es concentrarse en el cálculo de la probabilidad que tiene una pareja de cumplir años el mismo día, sin importar cuáles sean los integrantes de la pareja ni el día en particular. Supongamos que en nuestra fiesta se encuentran 23 personas. Se pueden formar 23 x 22 / 2 = 253 parejas diferentes entre ellas. Si no te has dado cuenta por qué calculamos ese número multiplicando 23 por 22, puedes pensar que para el primer integrante de la pareja hay 23 candidatos posibles, mientras que para el segundo, solo hay 22, pues uno de ellos ya forma parte de la misma. Ahora sí, calculemos la probabilidad aproximada de que en una habitación de n personas, al menos dos cumplan años el mismo día, desechando los años bisiestos y asumiendo que cualquiera de los días del año tiene la misma tasa de nacimientos que el otro. Comenzamos calculando primero la probabilidad de que “n” cumpleaños sean diferentes. 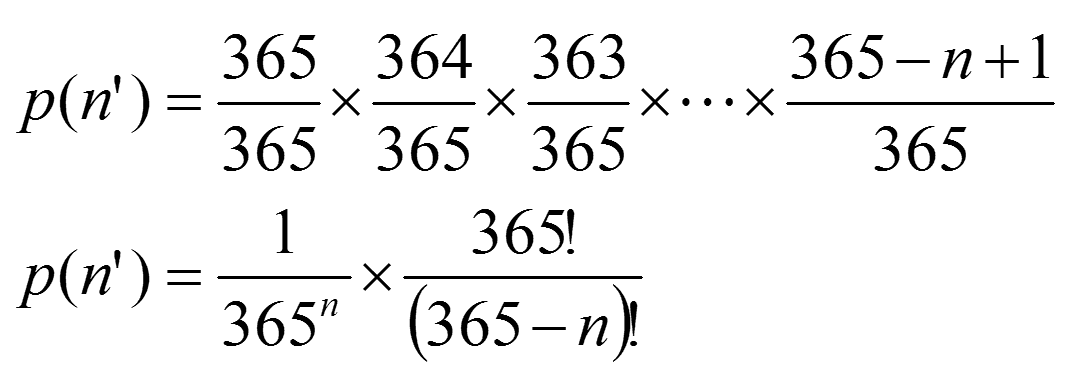Esta probabilidad es dada por la siguiente ecuación:
Lo que representan esa serie de fracciones es el hecho de que la segunda persona no puede tener el mismo cumpleaños que el primero (364/365), la tercera persona no puede tener el mismo cumpleaños que las dos primeras (363/365), y así sucesivamente. Podemos simplificar mucho esa fórmula si utilizamos los llamados “números factoriales”. El “factorial” de un numero (“n!”) se obtiene multiplicando entre sí a ese número y todos los enteros menores a él. El factorial de 5, por ejemplo, se calcula haciendo 5! = 5 x 4 x 3 x 2 x 1 = 120. Si utilizamos números factoriales, la ecuación se puede escribir de la siguiente manera:
En la que “p” es la probabilidad de que dos personas no cumplan años el mismo día. Para encontrar el resultado que estamos buscando -la probabilidad que al menos dos personas tengan el mismo día de cumpleaños- debemos hacer 1-p. Si la ecuación es lo suficientemente complicada como para que no de te den siquiera ganas de intentar resolverla, no te preocupes: lo hemos hecho por ti. Para n = 23 se obtiene un valor de 0,507, o lo que es lo mismo, una probabilidad de alrededor de 50,7%.
La próxima vez que vayas a una fiesta en la que hayan otros 20 o 30 invitados puedes intentar averiguar si dos de ellos cumplen años el mismo día. Si son más de 50, hasta puedes tomar el micrófono y lanzar una apuesta sobre ello, con una gran probabilidad de ganar y volver a casa con la chica más bonita de la fiesta. Y si falla, puedes entretenerte calculando las posibilidades que había de que una catástrofe así ocurriese. ¿Te animas? -
¿Y tú, qué opinas?
-
#1Froster sábado, 31 de octubre de 2009, 13:38
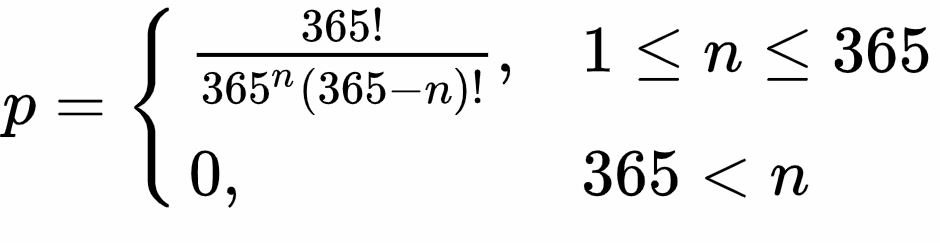
Ojo, estamos hablando del mismo día o de el mismo día. Que no es lo mismo, pues tenemos el mismo día (número) o el mismo día (número concreto en un mes concreto).
Aunque no deja de ser curioso, sería una propabilidad a cara o cruz. Otra cosa es que hablemos que sea la segunda opción... -
#2marshall_260 sábado, 31 de octubre de 2009, 13:53
Hola Froster!
Mismo dia es "mismo dia", mes incluido. Por ejemplo, dos personas que han nacido el 12 de febrero.
Saludos! -
#3Juan Sebastian Gamez Guarin sábado, 31 de octubre de 2009, 14:00
Se refiere a la posibilidad de que cumplan años el mismo día del mismo mes (por eso las operaciones se calculan sobre 365).
Muy interesante, y al igual que con la de la goma elástica y la del barco me he quedado a cuadros... -
#4Invitado sábado, 31 de octubre de 2009, 14:09
#1No se si soy demasiado tonto y no lo entiendo o mi logica me falla, supongo que puede variar de interpretaciones a la hora de resolverlo.
Desde mi punto de vista, un año tiene 365 dias, pues es como si tuvieras una bolsa con 365 bolas, y sacases 23 bolas, de una en una volvieindola a meter dentro, y segun "ESTA LOGICA" de cada 100 veces que lo experimentases, en 50 ocasiones saldrian por lo menos 2 bolas repetidas. IMPOSIBLE.
Es muy facil de demostrar, hazte un programita que aleatoriamente te saque numeros entre 1 y 365 y que lo repita 23 veces a ver que sucede. -
#5
-
#6lizzeth sábado, 31 de octubre de 2009, 14:13
Con 23 personas 50.7 % de probabilidades de volver a casa con la chica más linda de la fiesta (estrictamente hablando, con una chica, que sea justo la más linda sería una verdadera paradoja), pero guarda porque el porcentaje de catástrofe es del 49.3 % (1-0.507). Osea, redondeando, 50 % de posibilidades de irme acompañado contra otro 50 % de posiblidades de quedar como el ebrio del festejo que se subió al escenario para hablar de probabilidades!!
En una de esas si son más de 100 personas me animo!! jajajaja -
#7
-
#8GRiLLo sábado, 31 de octubre de 2009, 16:35
#4Ehm, creo que eso sería la posibilidad de sacar dos bolas iguales de una bolsa con 365 bolas. Y si hay una bola para cada día, como es que sacás 2 bolas iguales. Claro que sería imposible. La ecuación no la entendí mucho, pero a simple vista uno se da cuenta que tu analogía... uhm, como que no es buena.
Y lo del programita pues... a mi me suena que es sólo un programa que saca SOLO 1 NUMERO y lo repite 23 veces (?) -
#9Ariel Palazzesi sábado, 31 de octubre de 2009, 16:40
#4Hola!
Estas en un error. El mismo que se explica en el articulo: ".. estamos calculando cual es la probabilidad de que alguno de los presentes cumpla años un día en particular..." y no lo que queremos calcular. En tu ejemplo de la bolsa con bolitas, deberias sacar 23x22 bolitas de una bolsa con millones de bolitas numeradas del 1 al 365, y ver si dos tienen el mismo numero. -
#10mortadelo_666 sábado, 31 de octubre de 2009, 17:04
#5Lee el articulo otra vez, ahí lo dice:
"...desechando los años bisiestos y asumiendo que cualquiera de los días del año tiene la misma tasa de nacimientos que el otro" -
#11juegos de estrategia sábado, 31 de octubre de 2009, 17:09
#7Erroneo, cada uno se comio medio pollo xD
-
#12marioml17 sábado, 31 de octubre de 2009, 17:11
En este problema lo que se hace es:
Probabilidad de 2 personas cumpleaños= 1-(probabilidad ninguno coincide/ todas las posibles)
Queda asi P(B)=1-(Variaciones 365 elementos tomados de n (n numero de personas)/ Variaciones con repetecion de 365 tomados de n)
1-V365,n/VR365,n
Saludos -
#13mortadelo_666 sábado, 31 de octubre de 2009, 17:18
Este artículo me recordó "la ley de los grandes numeros", ese calculo tan espectacular pero incomprandeido al mismo tiempo
Las probabilidades de que se cree vida "por si misma" en nuestro planeta tierra, son tan pequeñas que lo damos por descartado casi inmediatamente, pero al ver la enorme cantidad de universos y planetas que existen, todas esas pequeñas posibilidades de exito se van sumando y sumando, hasta que en un momento dado "lo imposible" se hace una "realidad"
-
#14mortadelo_666 sábado, 31 de octubre de 2009, 17:26
#1323 personas = 50%
60 personas = 99%
tengan cuidado!!!
Eso nos ASEGURA que incluso habiendo 60 personas, en 1 de cada 100 fiestas de cumpleaños a la que vayas, VAS A PERDER LA APUESTA y como ya dijeron en otro post mas atras:
"quedarás como el ebrio que se subió al escenario y se puso a hablar de probabilidades"
jajaja xD -
#15
-
#16nicolasg sábado, 31 de octubre de 2009, 21:12
el como el comercial de NATGEO... "compartes tu cumpleaños con 17 millones de personas" si en la tierra existen mas de 6 mil millones de habitantes, todos nacen en dias del año, si divides esa cantidad entre los 365 dias, da ese resultado mas o menos, las probabilidades son bien amplias, yo mismo tengo varios amigos que cumplen en la misma fecha que yo!
-
#17
-
#18Capitan Obvio domingo, 01 de noviembre de 2009, 00:46
Las probabilidades aumentarian mucho si las 23 madres fueran conocidas de edad similar que hubiesen tenido hijos en fechas similares....
Fuera de esto, yo conoci a una joven que tenia igual fecha de cumpleaños que la mia 26/12/1988 sin embargo en la hora de nacimiento la diferencia era de casi 14 horas (yo era mas joven XD) -
#19
-
#20Pedro domingo, 01 de noviembre de 2009, 01:40
#19Selita Evans, Alessandra Ambrosio, Gisele Bunchen, Adriana Lima y Karolina Kourkova
-
Cargando...
-
nuevo comentario
Nombre Campo obligatorio
Email Escriba una dirección de correo electrónico con el formato sunombre@ejemplo.com.
Campo obligatorio
-
