Todo comenzó en el año 1993, cuando un banquero y entusiasta matemático llamado Andrew Beal se encontraba investigando generalizaciones del último teorema de Fermat. En pleno estudio llegó a plantear una curiosa conjetura, con la base Aˣ+Bʸ=Cᶻ, donde «A, B, C, x, y, z» son enteros positivos con «x, y, z > 2», y «A, B, y C» deben tener un factor común primo. ¿Suena complicado? Pues no estás solo, porque desde hace más de 20 años existe un premio de un millón de dólares para quien lo demuestre por completo, o presente un contraejemplo.
La matemática es una herramienta maravillosa, algo frustrante para mucha gente, y una verdadera máquina de derretir cerebros bajo las condiciones correctas. Pocos ejemplos son tan contundentes como el número de Graham, tan grande que no alcanza el universo para escribirlo. Después hay cosas a las que simplemente podemos considerar bellas (digamos, el número áureo), perturbadoras (el argumento del juicio final), o raras hasta la médula (la máquina de Galton). ¿Qué tenemos aquí hoy? Bueno…
Damas y caballeros, la conjetura de Beal, formulada en 1993 por el matemático, banquero y jugador de póquer Andrew Beal. Al igual que muchos otros matemáticos, Beal decidió cruzar espadas con el histórico «último teorema de Fermat», pero a través de su trabajo llegó a un desafío muy similar: Aˣ+Bʸ=Cᶻ, donde «A, B, C, x, y, z» son enteros positivos con «x, y, z > 2», y «A, B, y C» deben tener un factor común primo. Una de las «soluciones» más citadas es 3³ + 6³ = 3⁵ con un factor común de 3, y otra es 7³ + 7⁴ = 14³, cuyo factor común es 7.
Ahora… ¿por qué es importante? ¡Por el dinero! Verás, la conjetura aún requiere de una prueba consolidada y verificada por terceros (el llamado «peer-review»), o como alternativa, de un contraejemplo. En 1997, Beal decidió ofrecer un premio de 5.000 dólares para quien logre cumplir con uno de estos objetivos, hasta que llegó al límite de un millón de dólares. Hoy, el premio se encuentra bajo la custodia de la Sociedad Matemática Americana, y como era de esperarse, cientos de entusiastas en la Web dicen haber cumplido con sus exigencias. Nadie lo logró…
Fuente: Fermat’s Library en Twitter
Fuente: Wikipedia




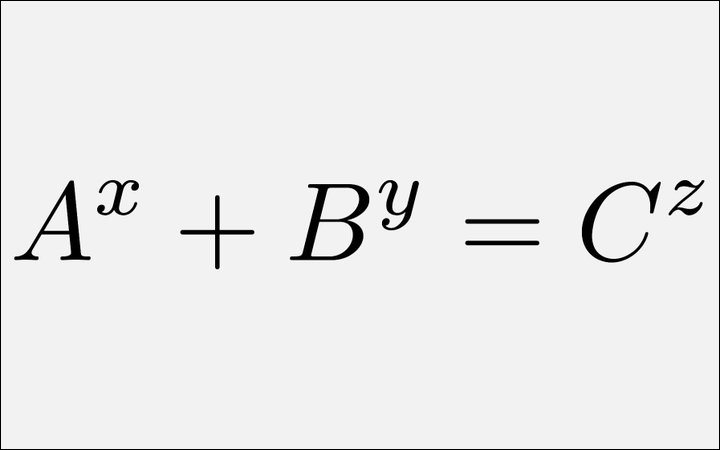

Hola amigo… voy a buscar más info de esta conjetura en la web, pero mientras tanto, no entiendo qué es lo que hay que demostrar, o cuál sería un contraejemplo válido. ¿Podés ampliar un poco? Gracias!
Llevo cerca de 1 año estudiando está conjetura y sacando pequeñas conclusiones.
Para poder hincarle el diente recomiendo empezar estudiando la prueba del último teorema de fermat, para lo cual necesitarás conocimientos de formas modulares (series de fourier, L funciones…) y curvas elípticas sobretodo. Una vez entendida ya puedes ponerte a mirar los pequeños resultados que se han obtenido de la conjetura de Beal.