El prolífico matemático John Horton Conway, muy conocido por sus aportes a la teoría de conjuntos , de nudos, de números, de juegos y de códigos, propuso el denominado “problema del ángel” en 1982. Tiene dos jugadores -el ángel y el demonio- y se juega sobre un tablero de ajedrez de tamaño infinito. Sus reglas son muy sencillas, y el diablo debe intentar confinar al ángel mientras este evita ser atrapado. Pero la verdadera dificultad de este problema consiste en determinar si existe una estrategia tal que asegure que uno de los dos contrincantes pueda ganar siempre.
Si hablamos de juegos de tablero, parece que cuando más simples son sus reglas, más atractivos resultan. El ajedrez, uno de los más complejos juegos de tablero que existen, tiene reglas tan simples que cualquiera puede aprenderlas en cinco minutos. Sin embargo, aplicarlas correctamente o encontrar una estrategia que asegure la victoria es una tarea enormemente compleja.
El problema del ángel
El problema del ángel, propuesto por el matemático John Horton Conway en 1982 en el libro Winning Ways (Maneras de ganar), pertenece a esta categoría. A pesar de ser más conocido por haber creado en 1970 el “juego de la vida”, Conway es un prolífico matemático que ha hecho aportes muy importantes en la teoría de conjuntos , la teoría de nudos, la teoría de números, la teoría de códigos y la teoría de juegos. El problema del ángel pertenece a esta última categoría.
En este juego, que en algunas publicaciones suele denominarse “Ángeles y Demonios”, participan dos jugadores, llamados respectivamente “el ángel” y “el diablo”. Se juega sobre una tablero de ajedrez de tamaño infinito, y ambos jugadores poseen características completamente diferentes. El ángel tiene “poder k”, donde “k” es un número natural igual o mayor que 1, y que se acuerda entre ambos participantes antes de comenzar el juego. Al comenzar, el tablero solamente contiene dos fichas: el ángel, en el centro del mismo (aunque al ser infinito, no tiene mucho sentido hablar de “centro”) y el diablo en cualquier otra casilla.
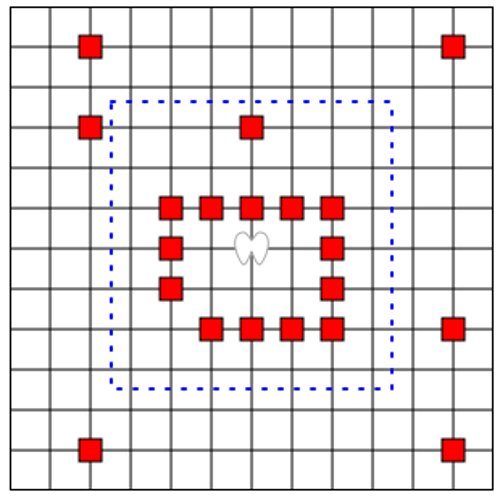
En cada turno, el ángel salta a otra casilla vacía, con la condición de que dicha casilla -moviéndose como lo haría un rey en el ajedrez- se encuentre a “k” casillas de su posición anterior y no esté marcada. Cuando es su turno, el diablo puede “marcar” una casilla cualquiera en la que no esté el ángel. En sus movimientos el ángel puede saltar sobre casillas bloqueadas, pero no puede acabar su recorrido sobre una de ellas. El diablo gana si logra que el ángel no pueda moverse, y el ángel gana si puede sobrevivir indefinidamente. La pregunta del millón es: ¿Puede un ángel con poder suficientemente alto ganar?
Para asegurar que existe una estrategia ganadora deberíamos demostrar que, o bien el diablo puede forzar una victoria en un número finito de jugadas, o que el ángel siempre dispone de un movimiento al que puede recurrir para evitar perder, en cuyo caso su “estrategia ganadora” sería tan simple como escoger siempre este movimiento. Lamentablemente, la solución dista mucho de ser fácil de encontrar.
El mismo Conway ofreció una recompensa por una solución general a este problema, que a pesar de no ser excepcionalmente atractiva -unos 100 dólares por una estrategia ganadora para el ángel y 1000 dólares para una demostración de que el diablo puede ganar cualquiera que sea el poder del ángel- hizo que cientos de aficionados a este tipo de pasatiempos transpirasen sangre tratando de encontrarla. Al igual que ocurre con otros juegos de tablero, es posible aplicar las reglas del problema del ángel a tableros de más dimensiones. En efecto, y aunque el juego original estaba pensado para tableros bidimensionales, las primeras demostraciones de estrategias exitosas (pero parciales) se encontraron para dimensiones mayores a dos.
En tres dimensiones se pudo demostrar que si el ángel se mueve siempre aumentando su coordenada Y, y el diablo sólo puede jugar moviéndose sobre dos planos, entonces el ángel tiene una estrategia ganadora. Por supuesto, nadie que jugase “de verdad” con el diablo se iba a limitar a mover de una forma más tonta, por lo tanto el ángel estaba muy lejos de tener una estrategia segura en su poder. Poco después se demostró que el bueno de la película podía ganar en 3D, siempre que su poder fuese mayor o igual que 13, sin importar de qué forma se moviese el diablo.
En cuanto al problema original, en dos dimensiones, fue el propio Conway quien hizo los primeros avances hacia la demostración buscada. En 1982 demostró que un ángel con k=1 siempre pierde frente al diablo. Ese mismo año también encontró que si el ángel nunca disminuye su coordenada Y, entonces el diablo siempre puede ganar. Por último, en 1996, demostró que si el ángel siempre aumenta su distancia desde el punto de origen, entonces el diablo tiene una estrategia ganadora. Las situación, evidentemente, no pinta nada bien para el ángel.
A pesar de todos los esfuerzos, no existe una demostración que -jugando sobre un tablero 2D- asegure la victoria de ninguno de los dos contrincantes. Esto, que puede ser visto como un fracaso por algún pesimista, es en realidad una prueba de lo entretenido que puede resultar un juego sencillo como este. La inexistencia -al menos hasta ahora- de una estrategia ganadora asegura que ambos jugadores tienen la oportunidad de ganar, algo indispensable para que un juego sea viable. Mientras que miles de jugadores disfrutan de sus partidas de “Ángeles y Demonios”, cientos de matemáticos se esfuerzan para encontrar una demostración que -quizás- ni siquiera exista.