La aparición de patrones complejos a partir de reglas relativamente simples es algo que hemos visto hasta el cansancio en la matemática. Verdaderos acertijos que dejan de cabeza a los expertos, dan lugar a toda clase de estudios, y son analizados durante décadas. El llamado «Problema de los Soldados de Conway» es un excelente ejemplo. Un campo partido en dos, soldados que siguen movimientos similares al del juego de damas, y un solo objetivo: Avanzar en territorio enemigo. A simple vista parece demasiado fácil, pero una vez que comenzamos a acumular movimientos, notamos que se trata de una batalla perdida…
John Horton Conway es uno de esos fabulosos matemáticos a los que regresamos una y otra vez. Lamentablemente nos dejó a principios de abril debido a complicaciones vinculadas a COVID-19, pero siempre lo recordaremos gracias a sus extraordinarios acertijos y rompecabezas. Es probable que algunos de nuestros lectores piensen el el «Juego de la Vida de Conway», o en el famoso «Problema del Ángel». También existe «Brotes», al que diseñó junto a su colega Michael S. Paterson, y el «Algoritmo del Fin del Mundo», que nos ayuda a calcular mentalmente qué día de la semana fue o será cualquier fecha del calendario.
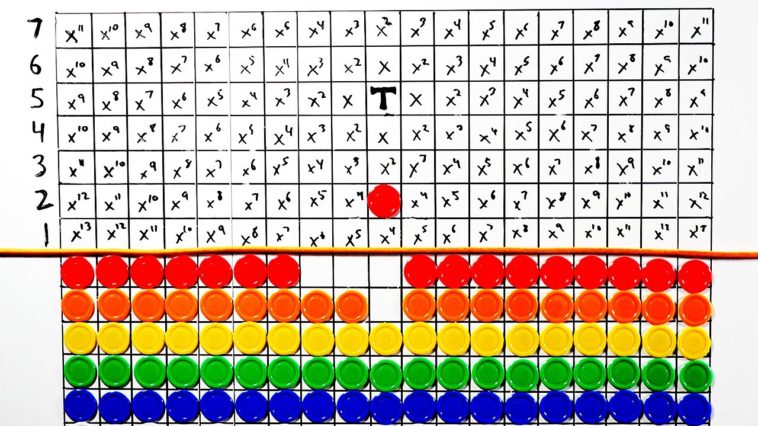
Hoy nos encontramos con su «Problema de los Soldados». Imagina un campo de batalla dividido en dos, y fraccionado en casillas como un tablero de damas o ajedrez. De un lado, tienes un grupo de soldados que sólo pueden avanzar como las fichas en las damas, o sea, saltando sobre otra y capturándola, pero con una restricción: Dicha captura se permite de forma vertical u horizontal, no en diagonal. El objetivo es avanzar en el campo enemigo tanto como sea posible. Ahora, es necesario destacar que el ejercicio no limita el tamaño del tablero, ni el número de soldados disponibles. 10, 20, 50, 750… no importa.
Entonces… las reglas son sencillas. ¿Por qué es «un problema»? En resumen, porque es imposible llegar a la quinta fila dentro de territorio enemigo. Para llegar a la primera fila, apenas necesitas dos soldados (un movimiento). Para la segunda fila, el número asciende a cuatro (tres movimientos). La tercera fila requiere ocho soldados (siete movimientos), y la cuarta veinte (19 movimientos). Pero la quinta fila quiebra todo. Todos los soldados que puedas tener, todos los movimientos que puedas hacer… son irrelevantes. La quinta fila es matemáticamente imposible de alcanzar… a menos…
… que hagamos trampa. Si se doblan un poco las reglas para permitir a los soldados saltar en diagonal, el acceso se extiende hasta la octava fila, pero no a la novena. Con una cantidad finita de movimientos, el resultado nunca es satisfactorio, sin embargo, Simon Tatham (creador de PuTTY) y Gareth Taylor demostraron que llegar a la quinta fila es posible con una cantidad infinita de movimientos. La gente de Numberphile le ha dedicado mucho tiempo al problema de los soldados de Conway, y uno de sus vídeos se extiende por más de 40 minutos:
Y detrás de todo este caos, de esta imposibilidad, se esconde nada menos que el número áureo, al que ya hemos explorado en su momento. De un tablero de damas con reglas simplificadas, a un desafío imposible que rebana cerebros y asombra incluso a los matemáticos más preparados. ¡Pero no te vayas! Como alternativa al infinito, también tenemos números muy grandes, comenzando por el Número de Graham (que no entra en el Universo), y la fabulosa Conjetura de Mertens.