El problema del caballo

El llamado “Problema del caballo” es un antiguo problema matemático relacionado con el ajedrez. Consiste en encontrar una secuencia de movimientos -válidos- de esta pieza para que recorra todas las casillas del tablero, visitando cada una solo una vez. Verdaderos ejércitos de matemáticos han encarado este problema, pero sigue sin conocerse el numero exacto de soluciones que existe. El problema ha sido planteado para tableros de diferentes tamaños y distintas condiciones iniciales, y sigue siendo tan atractivo como hace 1200 años.

A lo largo de los siglos, los matemáticos han utilizado el tablero y piezas del juego de ajedrez para plantear miles de acertijos, muchos de los cuales presentan semejante nivel de complejidad, que no han logrado ser resueltos ni siquiera abordándolos con los superordenadores más potentes.

El problema del caballo

El denominado “problema del caballo” es uno de los desafíos que involucran elementos del ajedrez más simples de enunciar pero más difícil de resolver. El reto consiste en poner un caballo en una de las casillas de un tablero de ajedrez vacío, y -respetando los movimientos válidos para esta pieza- recorrer cada uno de los casilleros sin pasar dos veces por el mismo, volviendo (o no) a la posición de partida. Si bien existen varios recorridos probados que satisfacen las condiciones enunciadas, lo cierto es que a pesar del esfuerzo de muchos matemáticos no se conoce con exactitud la cantidad de soluciones posibles para el problema del caballo.

Una de las primeras soluciones conocidas data del siglo IX. En efecto, en un manuscrito del árabe Abu Zakariya Yahya ben Ibrahim al-Hakim se encuentran documentados dos recorridos válidos. Uno de ellos pertenece a un jugador de ajedrez llamado Ali C. Mani y el otro a Al-Adli ar-Rumi, un aficionado del que se sabe también escribió un libro sobre una forma de ajedrez popular por esa época llamado “Shatranj”.

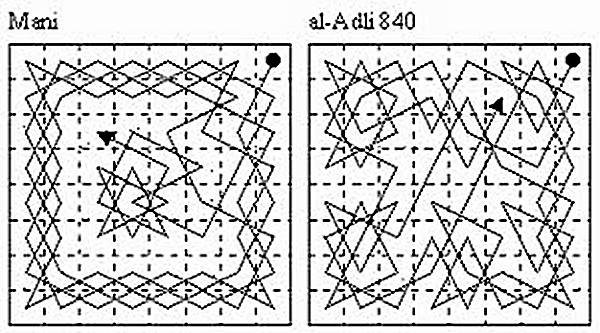
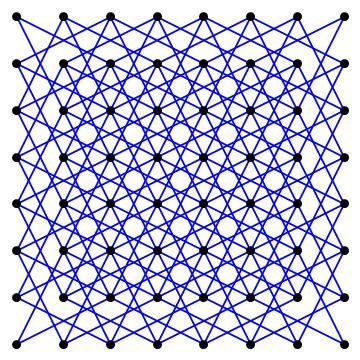
A lo largo de los siglos, el problema del caballo fue modificándose, dando lugar a distintas variantes. Por ejemplo, pueden utilizarse tableros de dimensiones diferentes a las 8×8 casillas tradicionales, o permitirse que la casilla de llegada no coincida con la de salida. Esta última variante facilita un tanto las cosas, y aumenta aun más la cantidad de soluciones posibles. Cuando el caballo debe llegar a la misma casilla de la que salió, se dice que el recorrido que efectúa es “cerrado”. As-Suli, otro árabe maestro de Shatranj, que basó su análisis en los trabajos anteriores de Al-Adli, encontró allá por el año 900 de nuestra era dos recorridos recorridos cerrados:

El primer estudio matemático importante sobre este problema se cree es el que efectúo el genial el matemático Leonhard Euler (1707–1783), quien presentó su trabajo a la Academia de las Ciencias de Berlín en 1759. En realidad Euler, una figura reconocida que publicó más de mil trabajos y libros brillantes durante su vida, sabía que la Academia ofrecía un premio de 4000 francos a aquel que pudiese arrojar algo de luz al problema del caballo. Si bien se conocían muchas soluciones, nadie había logrado estimar el número de ellas que existían ni un algoritmo que permitiese generarlas sin dificultad.

Los que habían abordado el problema sabían que encontrar una solución simplemente moviendo el caballo “al tanteo” era prácticamente imposible, pero tampoco eran capaces de encontrar un método que facilitase el proceso. Así las cosas, Euler encaró el problema y encontró que existían varios recorridos cerrados que ofrecían la ventaja de permitir comenzar por una casilla cualquiera del tablero y completar el recorrido a partir de ella. Lamentablemente, en el momento en que publicó su trabajo, Euler se desempeñaba como Director de Matemáticas de la Academia de Berlín, por lo que por una cuestión ética no pudo cobrar el premio.

Hoy sabemos que el número de recorridos posible es realmente muy grande. A pesar de haberse utilizado los más grandes ordenadores disponibles para buscar todas las formas en que el caballo puede recorrer el tablero, no estamos seguros de que los valores hallados sean correctos. En 1995, Martin Löbbing e Ingo Wegener pusieron a trabajar 20 ordenadores Sun -potentes para la época- durante cuatro meses y publicaron un documento en el que proclamaban que el número de recorridos posibles en un tablero de 8×8 era 33.439.123.484.294. Dos años más tarde, en 1997, Brendan McKay encaró el problema del caballo dividiendo el tablero en dos mitades y llego a un resultado algo menor: “solo” existirían 13.267.364.410.532 recorridos posibles. Para tener una idea de lo que significan estos números, basta saber que si un robot fuese capaz de mover el caballo para que complete un recorrido por segundo, demoraría más de 420 años en probarlos a todos.

¿Qué utilidad tiene para un jugador de ajedrez conocer estos recorridos? Muy poca. Pero esta clase de desafíos han impulsado a muchos aficionados o matemáticos a encarar problemas que finalmente suelen tener alguna aplicación práctica a la hora de encontrar rutas óptimas que pasen por un determinado número de lugares o que permitan -por ejemplo- ahorrar tiempo o combustible. Como sea, el  Problema del caballo ha logrado mantener interesados a los matemáticos durante siglos, y todo parece indicar que lo seguirá haciendo durante mucho tiempo. ¿No crees?

23 damas versus 39 caballos de ajedrez: ¿Quién gana?