No son pocos los que creen que un viaje en el tiempo solucionaría muchos problemas, pero a decir verdad, lo más probable es que los cause. En este breve acertijo publicado por TED-Ed sucede exactamente eso: Un profesor cruza por accidente un portal que lo envía a la prehistoria, y su asistente debe rescatarlo obedeciendo a una serie de condiciones muy específicas, combinando nódulos, entrelazamiento cuántico, y una teoría matemática en segundo plano. ¿Puedes ayudar?
El acertijo nos enseña al profesor Ramsey, demasiado enfocado y distraído a la vez, terminando de cabeza en un portal temporal que lo envía a la prehistoria. Su asistente quiere reaccionar rápido e ir al rescate, pero el problema está en la propia naturaleza del portal: Al cruzarlo se cerrará automáticamente, y debe llevar consigo los materiales para crear otro.
- El portal para volver al laboratorio requiere un mínimo de tres nódulos que se conectan automáticamente entre sí, formando un triángulo. El color de esas conexiones puede ser rojo o azul.
- La única manera de generar un portal estable de regreso al presente es que el triángulo tenga todos sus lados del mismo color, ya sea azul o rojo.
- Lamentablemente, los colores son definidos en forma aleatoria, y no hay forma de cambiar el color una vez establecido.
- Por suerte, existe una ventaja: Las conexiones entre nódulos pueden cruzarse sin inconvenientes.
- Sin embargo, el triángulo debe estar compuesto por un nódulo en cada esquina. Los triángulos formados por intersecciones flotantes no sirven.
- Como si eso fuera poco, la asistente debe trabajar con la cantidad más baja posible de nódulos, o el portal se volverá inestable.
La pregunta es: ¿Cuántos nódulos debe llevar la asistente del profesor Ramsey al pasado para garantizar la formación de un portal triangular con todos sus lados azules o rojos?
(N. del R.: El vídeo tiene subtítulos en español)
Resolviendo el acertijo del viaje en el tiempo
El acertijo se basa en la llamada teoría de Ramsey, desarrollada por el matemático y filósofo Frank Plumpton Ramsey a principios del siglo XX. La teoría puede ser resumida de esta forma: «¿Qué tan grande debe ser una estructura para garantizar que una propiedad en particular se mantenga intacta?» En este caso, necesitamos un triángulo con todos los lados azules o rojos, usando la menor cantidad de nódulos.
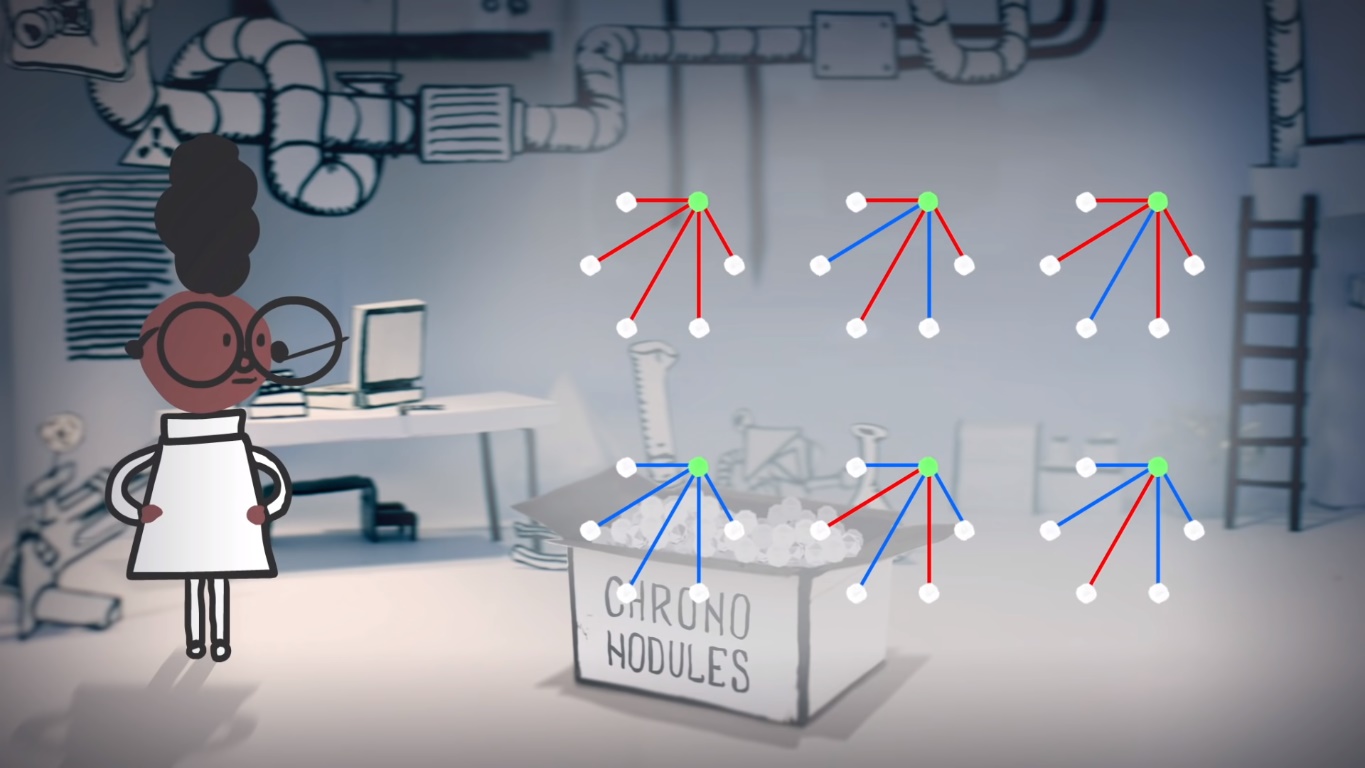
El vídeo hace una breve exploración por fuerza bruta: Al usar 3, 4 o 5 nódulos, existe la posibilidad de un patrón incompleto que deje a nuestros inesperados viajeros atrapados en el pasado. Sin embargo, la respuesta llega con el uso de seis nódulos. Independientemente de la configuración inicial, con seis nódulos siempre habrá un triángulo azul o rojo que funcionará como portal de regreso.