Ya sabes que nos encanta derretir cerebros aquí en NeoTeo, y una de nuestras técnicas favoritas para hacerlo es presentar paradojas. Algunas nos tocan muy de cerca, como es el caso de la paradoja de la elección, mientras que otras afectan de forma exclusiva a los robots.
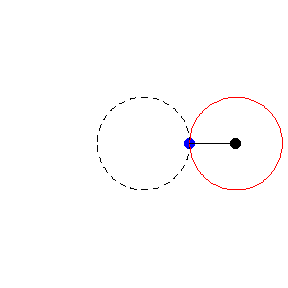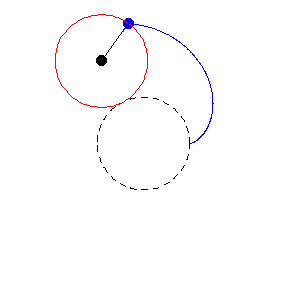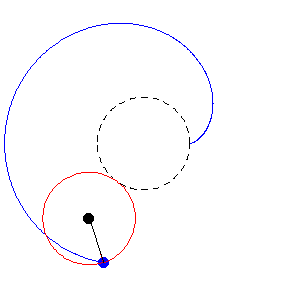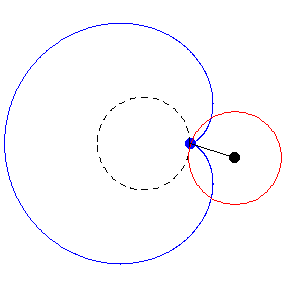
Hoy vamos a presentar una paradoja que puedes reproducir en casa fácilmente. Todo lo que necesitas es un par de monedas idénticas, colocadas en contacto y con la misma posición. Si haces girar a una de las monedas siguiendo la circunferencia de la otra, ¿cuántas rotaciones completa?
La paradoja de la moneda que gira suele estar asociada a una pregunta que fue publicada en un viejo examen SAT del año 1982: Un círculo denominado «A» tiene un tercio del radio del círculo mayor «B». El círculo «A» rueda siguiendo la circunferencia total del círculo «B», hasta regresar a su posición original. La pregunta es: ¿Cuántas rotaciones completó el círculo «A»?
Casi todos los participantes escogieron como respuesta «3», porque el círculo «B» tiene tres veces la circunferencia del círculo «A». A simple vista cualquiera les daría la razón, sin embargo, el ejercicio sufrió dos problemas: La respuesta correcta no es 3, y ni siquiera estaba disponible dentro del multiple choice. Entonces… ¿cuál es el truco?
La paradoja de la moneda que gira
Para descubrirlo hay que usar dos monedas idénticas, y hacer girar a una siguiendo la circunferencia de la otra, tal y como sucede en el ejercicio de los círculos. La sorpresa (por así llamarla) es que la moneda completa una rotación a mitad de camino, y una vez que regresa a la posición original, las rotaciones finales son dos. La paradoja de la moneda en todo su esplendor.
Lo que sucede aquí es que hay dos movimientos en juego: Rotación y revolución. La moneda en movimiento completa una revolución alrededor de la moneda central, pero también rota sobre su eje al hacerlo.
Por esa razón, si llegas a encontrar un ejercicio similar en una evaluación, la respuesta es «n+1», o sea, hay que sumar una revolución al final. Eso te permitirá escapar con facilidad de la paradoja, independientemente del tamaño de los círculos.
¿Quieres más paradojas o dilemas para seguir? Si la respuesta es afirmativa, puedes repasar a un clásico como el dilema del prisionero, el experimento mental de la habitación china, la paradoja del cumpleaños, y por qué es mala idea repartir la cuenta al cenar.
(Del Archivo de NeoTeo, artículo originalmente publicado el 31 de julio de 2019)








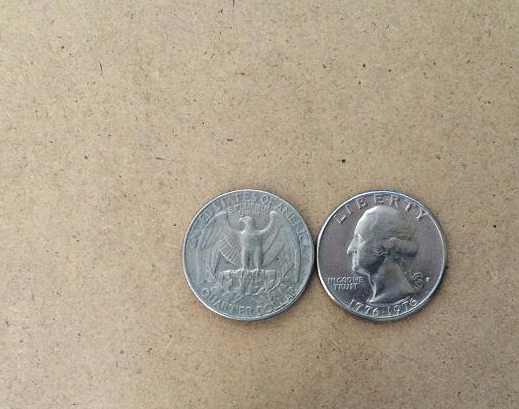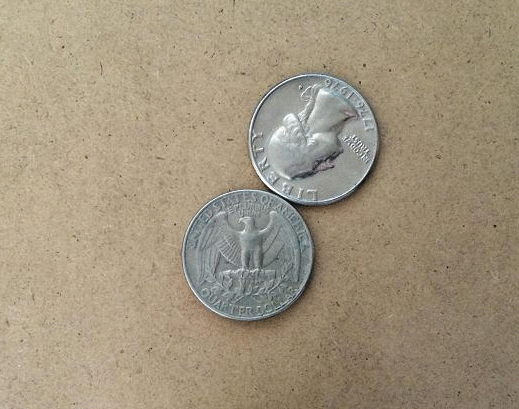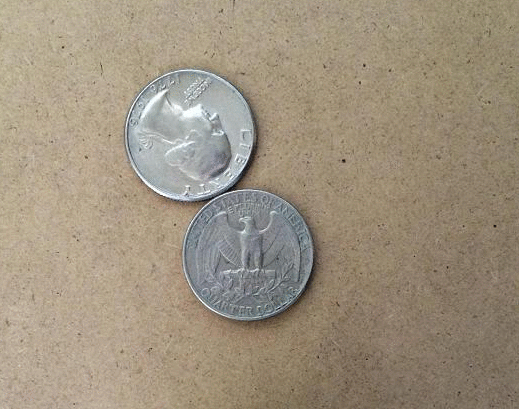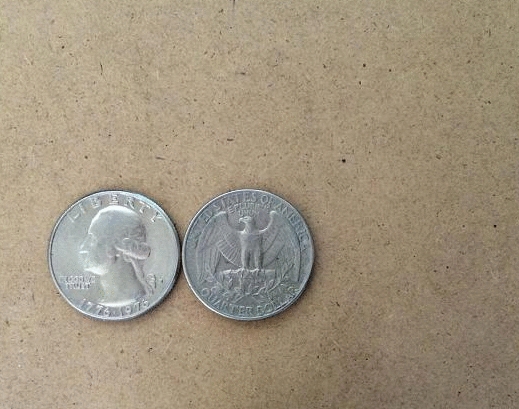
Por qué se habla de 3 veces la circunferencia cuando en realidad es tres veces el radio???
No es lo mismo, no?
La longitud de la circunferencia es 2(pi)R. luego si el radio es 3R, la longitud es el triple, y ya está
Algo parecido, aunque no idéntico, ocurre con los movimientos de la Tierra: rotación entorno a a su eje, traslación alrededor del Sol: por esta razón se distingue entre día sidéreo y día solar. El día solar es algunos minutos más largo que el día sidéreo. Esto significa que, al final del año, la Tierra ha girado 366 veces entorno a su eje, pero nosotros solo hemos contabilizado 365 días (aproximadamente)
Pero el punto en una circunferencia no es lo mismo que posición original, son dos cosas muy diferente
Considerando más detenidamente el tema, acabo convencido de que todo es un “fake”. La demostración gráfica que se hace, de una circunferencia girando alrededor de la otra, es ridícula: a la circunferencia exterioor se le puede hacer girar entorno a su eje todas las veces que se quiera, mientras gira en torno a la otra circunferencia, sin que nuestro ojo (cerebro), que es muy manipulable, se percate de ello. Aunque bastaría señalar que algo así ignoraría las leyes de la lógica.
Qué mal lo habéis explicado esta vez. A ver si yo se explicarlo mejor.
En el caso de los dos monedas iguales, el tema es que suponemos que la moneda que gira hace el giro desde su centro y por tanto consideramos que como son iguales tiene le mismo radio … y ahí esta el error, la moneda que gira su centro describe una circunferencia al rededor del centro de la moneda que esta quieta y ese centro de la moneda que gira reproduce una circunferencia pero no del radio de la moneda sino del doble del radio de la moneda, por tanto por eso da dos vueltas ya que su radio no es R sino 2R.
El error es que consideramos el borde de la moneda como centro de referencia => 2*pi*R/2*pi*R=1 … MAL por que es 2*(2*pi*R)/2*pi*R=2
Asi creo que se entiende mejor, el error es considerar mal el punto de referencia y la distancia que este recorre con la primera formula consideramos que el punto de referncia es el borde de la moneda con el segundo consideramos el de verdad lo que recorre el centro de la moneda que se mueve, que esta R mas alejado del centro de la moneda que no se mueve.
POr eso, siempre vemos la misma cara a la LUna: porque gira N veces=1 y debería ser N+1.
Los estudiantes de ingeniería mecánica lo saben, cuando calculan engranajes “satélites y planetarios” (por ejemplo, el diferencial de un coche) saben que siempre se debe añadir ese +1 a la vueltas que realiza el satélite en función del numero de dientes (z) que tienen y que a su vez es función del diámetro.