El “teorema de los cuatro colores” asegura que solamente se necesitan cuatro colores diferentes para colorear un mapa cualquiera, de tal modo que dos regiones cualesquiera, que compartan una frontera común, tengan colores diferentes. Todos hemos visto algún mapa pintado de esa manera, pero por sencillo que parezca, determinar formalmente qué cuatro colores bastaban para colorear cualquier mapa ha mantenido ocupados a los más importantes matemáticos durante casi un siglo y medio. Esta es la historia.
-
-
A menudo los problemas que parecen demasiado simples resultan ser un hueso duro de roer cuando se intenta obtener una demostración matemática o una generalización que incluya todos los casos posibles. El coloreado eficiente de mapas es uno de ellos, y ha dado lugar al llamado “teorema de los cuatro colores”, que dice más o menos lo siguiente: "En un plano o en una esfera no se necesitan más de cuatro colores para colorear un mapa de forma que dos regiones adyacentes, es decir, que compartan una frontera ―una línea, el punto no cuenta― no queden coloreadas del mismo color". Seguramente has visto a lo largo de tu vida una gran cantidad de mapas, y sin importar la complejidad del mismo, siempre deben haberte mostrado los países o regiones que representan usando solamente cuatro colores diferentes. Los fabricantes de mapas y los cartógrafos sabían ya desde la época del renacimiento que les bastaban esa cantidad de colores para evitar que dos estados vecinos quedasen pintados con el mismo color, pero hasta el siglo XIX nadie creyó que este sistema tuviese relacionado con las matemáticas y -mucho menos aún- podía encontrarse una demostración que confirmase que era válido para cualquier tipo o tamaño de mapa.
El coloreado eficiente de mapas ha dado lugar al “teorema de los cuatro colores”
El asunto de los cuatro colores se convirtió formalmente en un problema matemático recién en 1850. El responsable de otorgar esa “categoría” al problema que enfrentaban los cartógrafos fue un estudiante inglés llamado Francis Guthrie, quien intuyó que el mecanismo empleado podía ser demostrado. Dado que el problema superaba su formación matemática, lo comentó con su hermano Frederick, quien había sido alumno del prestigioso matemático inglés Augustus De Morgan. Nacido en la India en 1806, De Morgan fue el primer presidente de la Sociedad de Matemáticas de Londres y tutor de la genial Ada Lovelace. Fue además el autor de las leyes fundamentales del álgebra de la lógica que llevan su nombre (“La negación de la conjunción es equivalente a la disyunción de las negaciones” y “La negación de la disyunción es equivalente a la conjunción de las negaciones”), por lo que a priori parecía la persona indicada para demostrar este teorema, que fue inicialmente conocido con el nombre de “problema de Guthrie”. Sin embargo, no pudo hacerlo.
Mapa político de España.
Lejos de olvidarse del problema que su alumno le había planteado, De Morgan consideró que “el problema del coloreado de mapas” era lo suficientemente interesante como para enviarle una carta a su colega Sir William Hamilton, quien era famoso por postular la estructura de los números cuaterniónicos. La leyenda cuenta que un día de 1843 Hamilton paseaba por el puente de Brongham, que cruza el canal Real de Dublín y, de repente, en un momento de inspiración, comprendió la estructura de los cuaterniones. De inmediato grabó sobre una piedra utilizando su navaja la idea. Los cuaterniones resultarían fundamentales para edificar la física relativista y cuántica, y para demostrar el teorema propuesto por Lagrange según el cual cualquier número entero puede escribirse como la suma de 4 cuadrados perfectos. Hamilton estaba en la cumbre de su carrera -todavía no había sido afectado por la adicción al alcohol que terminaría enterrándolo en 1865- por lo que De Morgan tenía la esperanza de fuese capaz de demostrar el “teorema de los cuatro colores”. Sin embargo, el matemático nunca se ocupó del problema, o bien lo intentó y no pudo resolverlo.
Nada impide usar más colores, pero 4 son suficientes.
Pero De Morgan nunca se olvidó del asunto, y con frecuencia se lo mencionaba a otros matemáticos. Incluso algunos historiadores creen que él es en realidad el autor de artículo anónimo incluido en un ejemplar de 1860 de la revista Athenaeum que trata del problema de los cuatro colores, que se considera la primera referencia publicada sobre de dicha conjetura. En 1860 el teorema ya había cruzado el océano, y varios matemáticos norteamericanos se habían puesto a trabajar para resolverlo. El filósofo y científico Charles Sanders Pierce fue uno de los que primero se ocupó de él en ese continente. En 1878 el matemático Arthur Cayley publicó un artículo llamado “On the colourings of maps”, en el que exponía a sus colegas el problema y enunciaba las dificultades que tenía su demostración. Al año siguiente la revista Nature anunció que el problema de los cuatro colores había sido resuelto por el abogado inglés Alfred Bray Kempe. Su demostración de que las regiones de un mapa plano cualquiera pueden pintarse con cuatro colores se incluyó en un ejemplar de la revista American Journal of Mathematics ese mismo año, y durante algún tiempo el problema se consideró resuelto. Habían transcurrido casi 30 años, durante los cuales las mentes más brillantes de la época atacaron el problema, para llegar a esta solución. Sin embargo, el fin de esta historia aún estaba por llegar.
A pesar del trabajo de los matemáticos, algunos cartógrafos se equivocan al pintar.
Alfred Bray Kempe fue nombrado Fellow de la Royal Society gracias a su trabajo, y se dedicó a ampliar los alcances de su artículo original. Otros matemáticos también colaboraron en esta tarea, y presentaron demostraciones alternativas. Incluso Lewis Carroll se interesó en el asunto y terminó desarrollando un juego para dos personas en la que cada jugador diseñaba un mapa con determinadas características, que el otro debía colorear ajustándose al uso de cuatro colores. Pero la dicha de Kempe se vio amenazada cuando en 1890 Percy John Heawood encontró un grave error en la demostración de abogado. Heawood escribió un artículo (“Map-colour theorem”) y presentó un mapa de 18 regiones que a, pesar de poder ser coloreado con solo cuatro colores, demostraba que el trabajo de Kempe distaba mucho de ser general. Poco tiempo después, un mapa “rebelde” de solo 9 regiones terminó con lo que quedaba de la demostración de Kempe. Nuevamente estábamos como en 1850, aunque Heawood demostró que cualquier mapa puede colorearse con cinco colores y que tres no son suficientes, el número empírico de cuatro utilizado por los cartógrafos desde hacia siglos seguía resistiéndose a los esfuerzos de la comunidad matemática.
El teorema, en Wikipedia
Es imposible dibujar un mapa que no se pueda pintar con solo cuatro colores.
Todo este revuelo sirvió para que el problema adquiriese tanta fama que se lo propuso a través de la London Mathematical Society (Sociedad Matemática de Londres) como “un problema importante a resolver.”En 1976, ciento veinticuatro años después de que Guthrie les complicase la vida a cinco o seis generaciones de matemáticos, dos especialistas de la Universidad de Illinois (EEUU) utilizaron un ordenador Cray para colorear 1900 tipos de mapas distintos y -luego de trabajar durante 1200 horas- se comprobó que no era posible dibujar un mapa que no se pudiese pintar con solo cuatro colores. Pero, a pesar de su esfuerzo, Kenneth Appel y Wolfgang Haken no habían conseguido una demostración en el sentido matemático, solo utilizaron la “fuerza bruta” del Cray para comprobar una gran cantidad de mapas. Nunca podríamos estar seguros de la inexistencia de un retorcido diseño que escapase al teorema de los cuatro colores. Este dilema siguió torturando a los matemáticos durante dos décadas más, hasta que por fin -en 1996- Neil Robertson, Daniel Sanders, Paul Seymour y Robin Thomas, todos de la Escuela de Matemáticas del Instituto Tecnológico de Georgia (EEUU) encontraron una demostración que, al menos hasta hoy, es aceptada por todos sus colegas. Hubo que esperar 150 años para que el teorema de los cuatro colores, un problema que todos los cartógrafos habían resuelto en la práctica, pudiese ser demostrado matemáticamente.
-
¿Y tú, qué opinas?
-
#1ZeK005 jueves, 08 de julio de 2010, 18:38
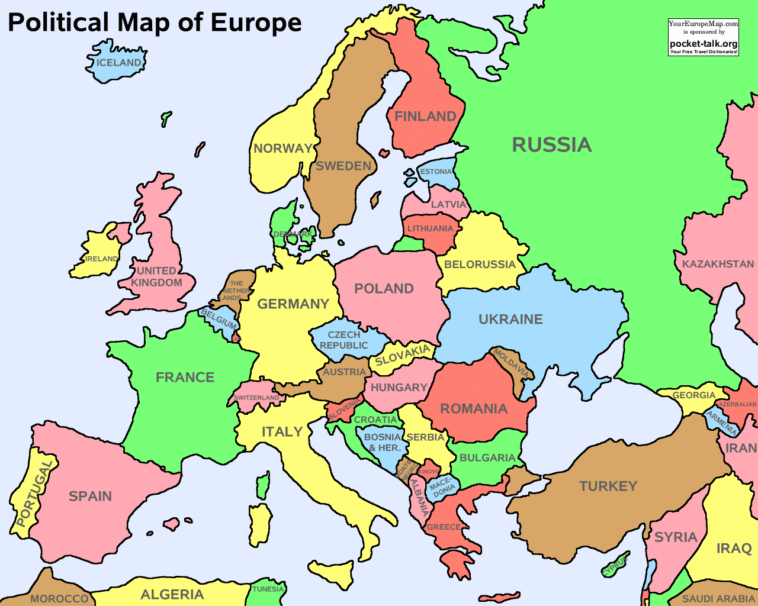
Muy buen dato y esto es asi ya que no existen en el mundo puntos donde se junten muchas fronteras al mismo tiempo (ejemplo el punto tripartito entre Paraguay, Brasil y Argentina). En este caso, los 3 paises deben tener colores distintos.
Si existiera en el mundo (y no se si existen) una cuadruple frontera, entonces se necesitarian 4 colores obligatoriamente. Extrapolando se nota obviamente que si llegara a existir una quintuple frontera seria SI O SI necesario usar 5 colores. Entonces la pregunta resulta en.... ¿Existen puntos geograficos en el mundo que 4 o mas regiones compartan al mismo tiempo? -
#2
-
#3
-
#4cronosferatu jueves, 08 de julio de 2010, 19:06
http://i30.tinypic.com/5osej4.jpg
-El pais nº 4 rodeo a los demas paises.
-Luego de una guerra entre los paises nº 2 y 3; 3 le permitio a 2 un pedazo de su tierra infertil para que 2 pueda hacer negocios con 4.
-Pais nº 1 esta pintado ahi xD, aun en frontera con pais 3.
-Pais ?, no sabe de que color pintarse.
Creo que este mapa esta bien hecho, aun que tal vez haya algun error por ahi (dibujando el mapa me encontre con varios errores que tuve q arreglar).
-
#5radamanto3 jueves, 08 de julio de 2010, 19:09
#1EN un capitulo de los Simpsons, los simpson se unieron de las manos para que cada simpson estuviera en un estado.
-
#6jesús jueves, 08 de julio de 2010, 19:24
#2Corrigo mi comentario anterior, cometí un error asignando colores a mi mapa fictisio. Hasta ahora si que me parece imposible llegar a dibujar un mapa que necesite más de 4 colores.
-
#7marshall_260 jueves, 08 de julio de 2010, 19:26
Hola Zek005!
El tema queda resulto en el enunciado el problema:
"En un plano o en una esfera no se necesitan más de cuatro colores para colorear un mapa de forma que dos regiones adyacentes, es decir, que compartan una frontera ―una línea, el punto no cuenta― no queden coloreadas del mismo color".
Fijate que el "punto" no se considera. En caso de que 8 paises (o el número que quieras) tengan un solo punto en común (como el centro de una pizza cortada en 8 porciones), bastarian solo 2 colores....uno para un pais, el siguiente con el otro, y luego repetir hasta terminar. No se si soy claro sin mostrarte un dibujo, pero el problema de la "quintuple frontera" no exist... Leer más -
#8marshall_260 jueves, 08 de julio de 2010, 19:28
#4Hola!
Simplemente, pintas el del "?" de color violeta, y el bloque violeta que te queda a la derecha lo p¡ntas de marrón..... :)
Creo que el error que cometiste fue pintar primero el cuadrado de violeta, y luego dibujar el interior. ;)
Saludos! -
#9luchovl2 jueves, 08 de julio de 2010, 19:44
#1Me parece que no, porque dice que no se consideran los puntos como fronteras, sólo líneas adyacentes.
"que compartan una frontera ―una línea, el punto no cuenta―" -
#10
-
#11lito jueves, 08 de julio de 2010, 19:54
#8si hacemos eso el pais 4 al ser marron toparia con el pais 2 que ya es marron, el coloco en su enunciado que el pais 4 rodea a todos los demas paises
-
#12Ardemion jueves, 08 de julio de 2010, 20:23
#4ya q me da lata ponerle colores y hacer un dibujo xD, lo digo con numeros
[...]
al final una imagen vale m{as que 1000 palabras XD
http://i32.tinypic.com/2v1olzc.jpg
saludos -
#13
-
#14gunn jueves, 08 de julio de 2010, 20:32
A mi lo que me parece raro es que seamos capaces de crear un software que pinte 1900 mapas usando 4 colores, y no entendamos por qué el algoritmo que los pinta no puede hacerlo con 3 y que sobren colores si se usan 5. Es como crear una inteligencia artificial sin entender como funciona la mente humana. Me desconcierta.
-
#15
-
#16
-
#17chipy jueves, 08 de julio de 2010, 22:18
#16Mintirooosoooo! :]
http://img3.imageshack.us/img3/6366/h4jylw0z.png -
#18leti_301 jueves, 08 de julio de 2010, 22:58
Detrás de todo este tema de los mapas y el coloreo, existe toda un universo de teoría sobre grafos planares y coloreo, para aquellos que estén interesados pueden echarle un vistazo.
-
#19victor141516 jueves, 08 de julio de 2010, 23:22
#17Aaaaah vale vale, que no habia pillado el concepto
-
#20julye viernes, 09 de julio de 2010, 00:22
Que curioso, yo de niño buscaba algo así (siempre perdía la mayoría de mis colores)... pero resulta que vivo en el estado de Oaxaca, en México, y colindamos con 4 estados distintos (Puebla y Veracruz al norte, Chiapas al este y Guerrero al oeste). Supongo que hay muchos casos como este, así que creo que esto de los 4 colores es insuficiente..
http://www.pickatrail.com/jupiter/location/north_america/mexico/map/oaxaca.gif -
Cargando...
-
nuevo comentario
Nombre Campo obligatorio
Email Escriba una dirección de correo electrónico con el formato sunombre@ejemplo.com.
Campo obligatorio
-
