Existe un buen número de métodos que los matemáticos y científicos emplean cuando deben resolver problemas complejos. Uno de los más versátiles y simples de entender es el denominado “algoritmo voraz” (Greedy algorithm). A pesar de que no siempre es capaz de encontrar una respuesta óptima, se lo utiliza con frecuencia dado que es muy rápido. Te contamos en qué consiste, qué ventajas tiene y cómo utilizarlo.
-
-
Para resolver un problema se deben seguir una serie de pasos. Estos pasos deben estar claramente definidos, sin importar que vayan a ser ejecutados por un ordenador o por un humano. La correcta definición de esos pasos garantiza que si se aplica el sistema dos veces a un determinado problema, la solución será la misma. Esta verdadera “receta” se llama algoritmo, y no es otra cosa que una secuencia de pasos ordenados y finitos con los que podemos resolver un problema determinado en un tiempo mínimo. El vocablo “algoritmo” proviene del latín “dixit algorithmus”, y éste a su vez del nombre de un matemático persa llamado Muhammad ibn Musa al-Jwarizmi.
La cantidad de recorridos posibles es igual al factorial del número de destinos.
Hay problemas que a pesar de tener un planteo sumamente sencillo, carecen de una solución que pueda ser considerada trivial. Imaginemos, por ejemplo, un viajante de comercio que debe recorrer 25 ciudades distribuidas por el interior de España ¿de que forma debería hacerlo para completar su trabajo recorriendo el menor número de kilómetros posible? El problema seguramente es de interés para un gran número de empresas, se puede definir claramente en pocas palabras, pero su solución demandaría a un ordenador varios años de trabajo. Esto se debe a que la cantidad de recorridos posibles es de 25! (25 factorial, o sea, 1 x 2 x 3 x 4 x 5 x ... x 24 x 25), es decir, hay 15.511.210.043.330.985.984.000.000 recorridos para probar y descartar antes de saber cual es el óptimo. Analizando mil millones de recorridos por segundo, demoraríamos 491,857,244 años en averiguar cual es el recorrido óptimo para nuestro viajante. Esto sirve para darnos cuenta de la importancia que tiene un algoritmo rápido, aun cuando no siempre sea capaz de encontrar el mejor resultado posible.
Para resolver un problema se deben seguir una serie de pasos, aunque seas Sheldon Cooper
El denominado “algoritmo voraz” sigue una estrategia sencilla pero eficaz. Simplemente, se trata de elegir la opción óptima en cada paso local, con la esperanza de llegar a una solución general óptima. En el ejemplo de nuestro viajante de comercio, cada paso podría ser tan simple como -estando en la ciudad “A”- dirigirse a la más cercana que aún no hayamos visitado. Una vez alli, repetir el procedimiento una y otra vez hasta que hayamos completado el recorrido. Seguramente no obtendremos un resultado óptimo, pero puede encontrarse un camino bastante bueno en un tiempo despreciable. Este tipo de algoritmo, a veces llamado ávido, devorador o goloso, es el que menos dificultades presenta a los investigadores que deben diseñar y comprobar el funcionamiento de diferentes estrategias. El nombre “voraz” se debe a que, en cada paso, el algoritmo escoge el mejor "pedazo" que es capaz de "comer" sin preocuparse de los pasos que restan hasta encontrar la solución. Un algoritmo de este tipo nunca deshace una decisión ya tomada: una vez incorporado, un “candidato a la solución” (ir de la ciudad “A” a la “B”, por ejemplo) formará parte de la solución. Y cada candidato rechazado es eliminado definitivamente.
Algoritmo voraz en Wikipedia
¿Que billetes debemos escoger?
Una vez aclarado el hecho de que los algoritmos voraces proceden por pasos, podemos ver en detalle como es su estructura. Se parte de un conjunto de candidatos que se encuentra vacío, es decir, no hay ninguna solución. Luego, en cada paso, se intenta añadir al conjunto el mejor candidato entre las soluciones que aún no han sido escogidas, a través de una función de selección. Luego de cada incorporación se comprueba si el conjunto de candidatos resultante es una solución del problema. Su esquema genérico es el siguiente:
función voraz(C:conjunto):conjunto
{ C es el conjunto de todos los candidatos }
S <= vacio { S es el conjunto en el que se construye la solución}
mientras ¬solución(S) y C <> vacío hacer
x <= el elemento de C que maximiza seleccionar(x)
C <= C \ {x}
si completable(S U {x}) entonces S <= S U {x}
si solución(S)
entonces devolver S
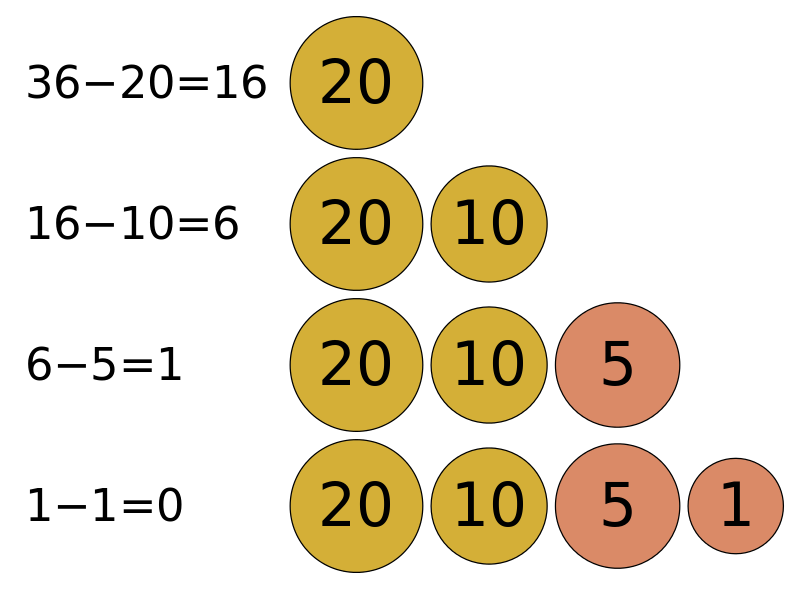
si no devolver no hay soluciónPara comprender exactamente su funcionamiento podemos aplicarlo a otro problema sencillo: Supongamos que disponemos de un grupo compuesto por cuatro tipos billetes de banco: diez billetes de 5, cinco de 10, tres de 20 y dos de 50. Tenemos que hacer un pago de 100 euros con el menor número de billetes posible ¿que billetes debemos escoger? La solución obvia consiste en utilizar dos billetes de cincuenta euros, pero ¿como llegaría a esa solución un ordenador? Muy simple: utilizando el algoritmo voraz. Al plantear ese problema, el “candidato” (c) sería un conjunto finito de billetes, la “solución” (S) el conjunto de billetes buscados y cuya suma es la cantidad a pagar, “completable” es la suma de billetes escogidos en un momento dado y que no supera la cantidad a pagar., y la “función de selección” no es otra cosa que la encargada de seleccionar el billete de mayor valor disponible en el conjunto de candidatos aún no seleccionados. En el primer paso se elegiría uno de los billetes de mayor valor disponibles (uno de 50). Luego de comprobar que no se llegó a la solución se tomaría nuevamente uno de los billetes de mayor valor disponibles (el restante de 50) y se comprobaría que hemos llegado a la solución. Simple de implementar, ¿verdad?.
-
¿Y tú, qué opinas?
-
#1
-
#2Edgar21 jueves, 19 de agosto de 2010, 16:33
No termino de entender esto de algoritmo voraz, me parece la manera mas logica de proceder por ejemplo con el de los viajes, elegis un punto y de ahi vas recorriendo por el mas cercano, o sea si ese es el planeamiento q gracia tendria ir de un punto al mas lejano, ni siquiera haces esa combinacion al empezar, asi q no seria nunca necesario el 25!
-
#3leidy urbano jueves, 19 de agosto de 2010, 16:43
Interesante, lo raro es que nunca lo había escuchado. En algunas presenta la solución optima, en otras aunque no garantiza la mejor selección si presenta una de las mejores altenativas. Gracias Neoteo.
-
#4
-
#5marshall_260 jueves, 19 de agosto de 2010, 16:54
#2Hola!
La forma de encarar un viaje que mencionas ("elegís un punto y de ahí vas recorriendo por el mas cercano") no es necesariamente la mas corta de efectuar el recorrido. De hecho, pocas veces es así. En Wikipedia (http://es.wikipedia.org/wiki/Problema_del_viajante) está extensamente explicado ;)
Saludos! -
#6shunkor jueves, 19 de agosto de 2010, 17:04
Hola gente, me encanta el articulo, me hizo acordar a cuando programaba en visual, ja, yo usaba cosas asi para soluciones, a ver, aca les dejo algo que hice recien, estoy en el laburo mucho mas no puedo pensar pero se que se puede hacer mas sintetico.
Bien, una persona nos pide que le paguemos 100 euros (o pesos aca en ARG.), y tenemos 2 posibilidades, una pagar justo con la menos cantidad de billetes como dijeron aca, y la otra que se me ocurrio agregar, pagarle dandole cambio, que a veces pasa..
Entonces lo que hacemos primero es ver los billetes que tenemos en la billetera, y suponiendo que ya los contamos quedamos que tenemos este dinero:
cinco = 10
diez... Leer más -
#7juancruzw jueves, 19 de agosto de 2010, 17:44
Me gustaría saber a quien se le ocurrió ponerle ese nombre,
como dijo ferba es la manera más lógica de proceder, bueno al menos la que el sentido común dictaría, pero tambien es cierto que no es la mejor, por ejemplo una experiencia personal.
Un día se me ocurrió lanzarme a la aventura de viajar de Guadalajara México a Manzanillo (puerto), por el simple hecho de olvidarme de una chica, sin dinero ni ánimos decidí irme de aventón; gran aventura, conocí gente muy pintoresca, lugares extraños, -un mini cementerio de avionetas, vagones de trenes abandonados, caminos desiertos y pueblos casi fantasmas-, yo iba aplicando una especie de variable de este algoritmo, lo que me resulte mejor... Leer más -
#8
-
#9radha2g jueves, 19 de agosto de 2010, 18:36
solo mire rapidamente el codigo
asi que, dejame hacer una pregunta, a ver si entendi el enfoque...
si tienes 5 billetes (o monedas) de $1, ... 1 billetes de 10$ .... 1 billete de $20 y 1 billete de $50
y si lo que debes pagar es $23?
Terminarias pagando $35 si tomas solo los billetes menores...
el acercamiento mas sencillo es utilizar los billetes mas grandes para salir de eso o la mayor tajada como dicen en el articulo, no siempre es la manera mas optima ya que podrias tener el cambio exato, pero a veces es sencillo usar el billete grande a tener que ponerse a verificar cuales billetes darle
sorry si me entendi mal pero e... Leer más -
#10MOYcano jueves, 19 de agosto de 2010, 18:44
Es genial... nunca lo había escuchado por ese nombre. Y no es tanto que sea un usuario intensivo de algoritmos pero de perdido les puedo mencionar tres o cuatro que funcionan por conceptos similares.
Pero en lugar de entrar en detalles les planteo otro problema de estos que la naturaleza resuelve zepetillones de veces al día: ¿cómo sabe un haz de luz en qué dirección avanzar? ¡Cómo sabe qué par de trayectorias rectilíneas le toma menos tiempo para llegar desde un punto en el medio A hasta otro en el medio B?
La respuesta, un tanto metafísica, suele basarse en un principio. "Hay que minimizar la acción" y en términos de integrales de trayectoria vienes y deduces la Ley ... Leer más -
#11
-
#12tornes jueves, 19 de agosto de 2010, 20:52
la distancia mas corta entre 2 puntos es una recta y san se acabó, para que dar tantas vueltas digo yo!!
-
#13Santiago jueves, 19 de agosto de 2010, 21:32
#12Si los cientificos y matematicos no les dieran vuelta a temas que parecen tan triviales no habrías podido escribir ese comentario ni leer este post. La curiosidad es lo que permite a la humanidad avanzar.
-
#14iron_ia jueves, 19 de agosto de 2010, 21:43
#7Al final, veo que no te sirvió para olvidarte de esa chica. Es más, recuerdas que ella fue el motivo por el que cual realizaste el viaje :)
...malditos algoritmos voraces grrr -
#15
-
#16
-
#17enaro viernes, 20 de agosto de 2010, 00:42
Tal y como lo recuerdo yo de la universidad, y corregidme si me equivoco, un algoritmo voraz es aquel que ofrece una solución no necesariamente óptima compuesta por un conjunto de soluciones parciales, de manera que, en cuanto el algoritmo se decide por añadir una cierta solución parcial, nunca vuelve atrás. Hay ciertos problemas que cumplen el principio de optimalidad, es decir, que una solución óptima al problema está compuesta por soluciones parciales óptimas (en el caso mencionado arriba, una solución parcial óptima seria ir de una determinada ciudad a su vecina mas próxima), aunque no suele ser así.
Donde si que se utilizan mucho los algoritmos greedy es en búsquedas de tipo... Leer más -
#18
-
#21juanes viernes, 20 de agosto de 2010, 09:20
#6Ojo, ten en cuenta que la cantidad de billetes es pequeña, imagina en España (¡Saludos Argentina!), como sabes tenemos monedas de 2, 1, 0.50, 0.20, 0.10, 0.05, 0.02 y 0.01 €. La gente no solo paga en billetes.
(Ademas es un ejemplo de comprension, para entender el anterior, lo de los billetes)
Tu algoritmo, seria demasiado lento, por los loop.
Se podria lograr con un unico bucle o loop, pero la duracion de este depende de la maquina que realice las operaciones, y la cantidad de dinero a devolver.
un saludo -
#24juanes viernes, 20 de agosto de 2010, 09:35
Una lógica multiple es buena para ayudar, pero no todas son buenas.
Elegir el camino mas corto, no es siempre lo mas lógico, ¿Por qué? Es fácil ¿Que es corto?
Quiero decir, imagina sales de un punto A, hacia B hay 100km y hacia C 50Km, bien elgimos C segun tú logica, pero ¿y si el camino mas corto desde C a otro es 250 km? y si desde b a otro el menor recorrido es 100Km ????
Es hay, la cantidad de calculos que debe realizar...
En la uni, escuche un comentario sobre el algoritmo perfecto (unico) de gps.
La maquina que resolviera el algoritmo mas corto entre dos puntos, pasando por x puntos, seria capaz de consumir la energia del sol. Y encima, no estariamos v... Leer más -
Cargando...
-
nuevo comentario
Nombre Campo obligatorio
Email Escriba una dirección de correo electrónico con el formato sunombre@ejemplo.com.
Campo obligatorio
-
